世界各国で国債の利回りが上昇し、債券への関心が高まっています。今回は債券投資の仕組みと利回り計算の仕方、金利が上昇すると債券価格が下落する仕組みについてみていきます。計算式が多い記事になりましたが、債券の大まかな仕組みだけでも理解いただければ幸いです。
- 債券投資では、利払い日に利子、満期日に利子と額面金額を受け取る
- 国債などの債券は、一般的に時価で購入でき、購入価格によって利回りに差が出る
- 後から利率の高い債券が発行されれば債券価格は下落、逆の場合は上昇する
債券投資の購入から満期までの流れ
国や企業などが債券を発行する場合、発行総額、発行価格、額面金額、利率、払込日、満期日などを記載した目論見書を作成し、投資家に提示します。投資家はその目論見書を参考に、その債券を購入するかどうか検討します。
債券購入後は、利払い日に利子を受け取り、満期日には利子と額面金額を受け取り、その債券への投資は終了します。
下の図が債券投資(5年満期の債券を満期まで保有)のイメージです。
①債券を発行価格で購入
②1年後~4年後は利子を受け取る
③満期時(5年後)は利子と額面金額を受け取る
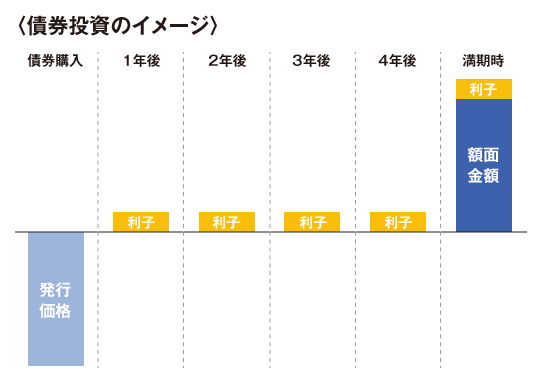
固定金利の債券では、利率が満期まで変わらないため、利子も一定で変わることはありません。
利子は以下の計算式で算出されます。
債券価格は、発行時は「発行価格」、発行後から満期までの間は「債券価格」、満期時は「額面金額」と名称が変わります。初めて債券を勉強される方にとって理解しづらい点のひとつになります。
額面金額は、満期時に受け取れる金額です。発行価格とイコールの場合と異なる場合があります。また、発行後から満期までの債券価格は、世の中の金利や景気の状況、その発行体(債券を発行した国や企業など)の財務状況の変化などにより変動します。
次に、債券価格と利回りの関係についてみていきます。
債券投資の利回りを計算してみよう
一般的に国債などの債券は、すでに発行された債券をその時の債券価格(時価)で購入できます。その場合、購入時の価格と額面金額との間に差が生じます。「購入価格<額面金額」の場合は満期時に値上がり益が得られ、「購入価格>額面金額」の場合は満期時に値下がり損が生じます。
そのため、受け取った利子と値上がり益(値下がり損)を合算して年間リターンを計算します。
その年間リターンが「利回り」になります。(発行金額≠額面金額の場合も同様です)
利回りの計算式は、
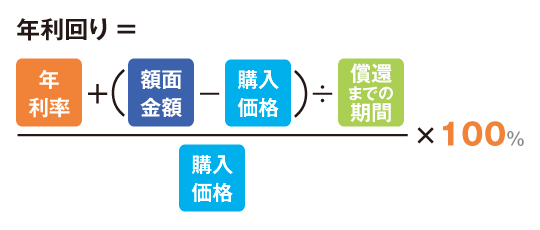
です。なお、満期前に売却した場合は「売却価格」が「額面金額」のところに入り、同じ計算式で年間の利回りを計算します。
例えば、償還まで3年、年利率2%、額面金額100万円の債券を97万円、103万円でそれぞれ購入した場合の利回りを以下の計算式で計算します。
97万円で購入した場合は、
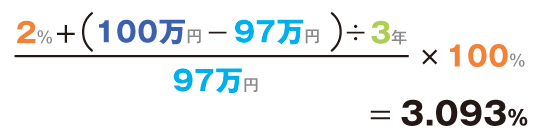
103万円で購入した場合は、
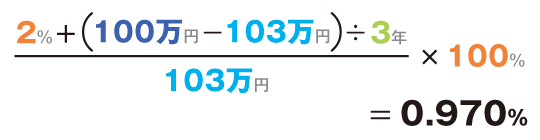
となり、購入価格によって利回りに差が出ます。
次に、満期までの期間に利率の違う債券が発行された場合の債券価格の動きについてみていきます。
金利が上昇すると債券価格が下落する
債券は、金利の変動などによって価格(時価)が変動します。
例えば、利率2%の債券が発行されている場合、世の中の金利が変動し、同じ発行体から2%より利率の高い債券が発行されると利率2%の債券の魅力が薄れ、債券価格が下落します。
逆に、世の中の金利が下がり、2%より利率の低い債券が発行されると利率2%の債券の魅力が高まり、債券価格が上昇します。
理論的には、利率3%の債券が発行された場合、それ以前に発行されていた利率2%の債券は最終利回り(満期までの利回り)が3%になるように債券価格の調整が行われます。
以下、2つのケースで調整された価格(理論価格)を計算してみます。
額面金額100円、利率2%の債券の満期前3年の時点で利率3%の債券が発行された場合、理論価格は約97.16円に下落します。
計算式は
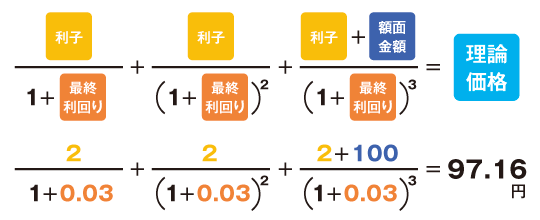
です。
同じ条件で、満期まで5年の場合の理論価格は約95.41円です。
計算式は、
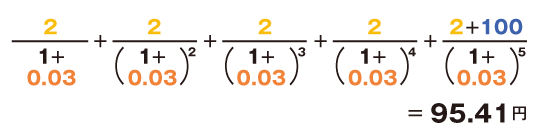
になります。
上の例の場合は、後から利率の高い債券が発行されたので債券価格が下がりました。また、満期までの期間が長い債券ほど価格の変動が大きくなります。後から利率の低い債券が発行された場合は、逆に債券価格は上昇します。
以上、債券投資の仕組みと利回り計算の仕方、金利が変動した場合の債券価格の動きについてみてきました。





















